The geometry of the dragonfly wing

  The folded surface of the dragonfly wing

A modeller’s experimental and morphological study

 

What do a ball of crumpled paper and a dragonfly’s wing have in common?

They are both constrained by the laws of the geometry of folded surfaces!

Translate by Dr JD Bell of Oxford

For further information refer to the page “geometrical principles”.

While researching different techniques for reproducing a dragonfly wing I came to realise the astonishing properties of its form.

The distinctive feature of the dragonfly wing is its strict adherence to shape with respect to its wingspan which is exceptional among insects. Put another way, it has the property of not bending under considerable stress, despite its length. Making my first model, of Orthetrum caerulescens on a 20:1 scale, I contented myself with reproducing the profile by heat forming on a mould that faithfully copied, without analysing it, the profile of the original. The heat forming method proved unsuccessful for making a life-size model of Anax imperator. I remembered then that I had studied folded surface theory in architecture. The distinctive feature of a folded surface is the simplicity of its construction and the ratio of weight to optimum formal stability. Applying this principle to the dragonfly wing showed that I was on the right track.

Surface folding theory works perfectly for the shape of the dragonfly wing and meets the constraints imposed.

At the time of writing, I know of no scientific publication on this subject. I apologise in advance if such a publication does exist. I should be delighted to if any author should get in touch.

 You can also look up the site enseeiht.fr on the theory of insect flight

There are also numerous references in worldLingo

 First structural analysis

Nature’s choices and their reasons:

 1-Rigidity of the wing: various consequences:

   - strengthening of the veining; increase of section, weight (eg short reach of bee and fly wing)

  - cylindro-conical form: concentration of stresses at the wing-root, poor aerodynamic response (plant environment)

  - folded form: sound distribution of stresses, structural lightness, rotational aerodynamics (principle envisaged, yet to be confirmed)

AO 1   Non-folded wing is not rigid

AO2    Wing with folds is made rigid by the three-dimensional structure thus created. This paper model has no veining and is maintained solely by folds that faithfully match the original.

Geometrical theory of folded surfaces

 1. Definition of a folded surface

- any plane surface not deformable in plan (see ‘geometrical principles’). For example, woven textile is deformable; a sheet of paper or steel is not deformable.

 This surface is folded in three-dimensional space by anetwork of folds alternately convex and concave.

A10

This example of folds was chosen for the design found in the dragonfly wing.

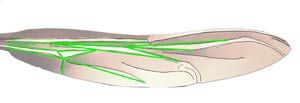A10a

The vein, shown in green, corresponds to the principal structural folds in the dragonfly wing.

Inversely, the shape of such a surface can be folded down flat without tearing

  A11

Interpolated note:it seems that the dragonfly wing alone has this arrangement of folds. In a bee’s wing, for example, the folds are of uniform shape.

    

The surfaces between the folds are not flat but convex, and not capable of being made planar.

Returning to the dragonfly:

 All the surfaces bounded by two folds are generated by straight lines. These surfaces are either planar, or conical or cylindrical.

A20

This simulation in folded cardboard, with its complex of curves and opposing curves reproduces exactly the surface of the dragonfly wing :

A90

The structural configuration (angle, length, orientation) of the folds obeys the rules of the geometry of spatial complexes. Each fold is directly defined by the set of folds of a convex polygonal surface. A single bordering surface is linked to the whole by a single straight fold allowing a degree of angular freedom.

A note about ‘geometrical principles’: on the dragonfly wing it can be seen that several sections of fold are incomplete. That seems to indicate that the folds of the wing form during specific development of the main veins. Could it be that the positioning of the main veins has determined the entire fold system of the dragonfly wing?

Evolution 

Preliminary remark: the dragonfly is known to be a member of a group of primitive insects. Titanophasma fayoli, a palaeodictyopteran, could reach a length of 50cm. Its geometrical form could have been decided at that time.

Primordial remark: As the example of the crumpled piece of paper showed, the process by which the folds we are concerned with were generated is very different from a process of evolving deformation of cells. Here adaptation of the molecular composition of the cells did not take place. It was the state of the wing body that underwent an architectural transformation. It is interesting to compare the folding of the dragonfly wing with structures in the earth’s crust resulting from tectonic pressure, notably in mountain ranges. It is as if the surface geometry of the wing has been deformed by exterior forces (a dynamic phenomenon at the wing root level) and not by an organic adaptation at cellular level.

This point is of particular importance, because it proposes a different theory for organic formation, or so it seems to me!

2.Properties

Given that the development of a folded surface is contained within a plane (the inverse of the folding operation) one can show geometrically that each folded surface, in the definition given above, is a three-dimensional structure of optimum material economy in its ratio of quantity of matter to spatial volume. In other words, for the same structural volume, the folded surface is the most economical in material (used) and in three-dimensional structural efficiency. This can be shown by triangulation on a plane of which each triangulated section is non-deformable. It follows that the whole form is structurally homeomorphic.

Given that each fold in terms of its angular, orientational and dimensional characteristics, is co-determined by all the other folds on the same total surface, any force applied to a particular fold has repercussions on all the other folds of that surface.

There is thus a related distribution of deformations and pressure over all, or part, of the surface of the wing.

Note that according to this law, each folded surface is limited in its angular deformation with a range of variation determined by the general configuration of the folds that comprise the whole. The range is considered later.

In the same way the angular amplitude of the set of folds may be controlled solely by the axial configuration of the costal veins at their origins.

It would be interesting to know whether the dragonfly is capable of varying these and if so what would be the aerodynamic consequences.

Detailed study of the dragonfly wing

 Any organism is at once more subtle and more complex than the geometric model with which it is compared. Thus in this study it will be necessary to take into account the flexibility of the membrane elements of the structure, the mechanism of initial deployment of the wing, and the potential of the creature to vary its geometry, either by muscular action or modification, if possible, of haemolymphatic pressure in the veins.

For obvious reasons we cannot go any deeper into these matters which are the reserve of specialists.

Topology of the folded surface of the wing

In light of the theory of folded surfaces, the dragonfly wing is seen to comprise different systems of folds that interpenetrate, compensate or oppose each other.

A. Distribution of the folds :

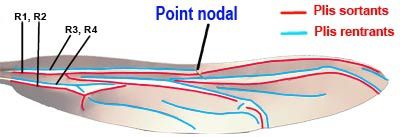A40a

First, the alternation of exiting and re-entrant folds may be noted (by convention the wing is always observed from above. Seen from below, the folds would obviously be reversed). The upper (exiting) folds are shown in red and the lower (re-entrant) folds in blue.

There are 4 rooted folds:

            2 exiting folds R1, R2

            2 re-entrant folds, R3, R4

It may be noted that no fold extends the full length of the wing. Notably, there is a break on a nodal point.

B. 3 stiffening groups

 - The structure can be divided into 3 similar group-systems

 These are the axial (polar) fold systems.

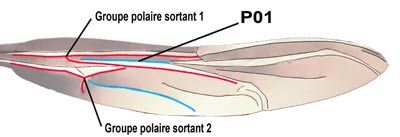A41

A42

Diagram of the axial (polar) system :

In an axial system all the folds converge towards a polar centre. A polar system requires at least two convergent folds (see geometrical principles). With up to three convergents the surface necessarily subdivides into conical curves.

With four or more folds, an alternation of exitings and re-entrants can be produced such that the surface is arranged as planes. This is found in the three group-systems listed.

1 and 2 formed by the wing’s rooted veins are termed exiting folds (the majority)

3 is formed from a non-rooted vein and its folds are the inverses of the two primary systems; it is termed a re-entrant fold.

It can be seen that exiting group 1 and re-entrant group 3 have a common fold, PO1. These two groups are thus geometrically interdependent.

 A third group 2bis a part of group2 and a rooted fold R4. It will be referred to later.

 Observation 1

Groups 1 and 2 direct the surface downwards while Group 3 directs the surface upwards. This may be confirmed very well by observing the wing in profile :

A60

Observation 2

The change of orientation occurs at the nodal point.

Observation 3

Groups 1 and 3 interconnected by fold PO1 form a structural system that controls the overall rigidity of the wing, from the root to the tip.

However, considering the hypothesis that angular variation of the wing occurs only by activation by the rooted veins this system is insufficient to control the angular variation of the whole structure.

It is axial group 2bis, formed from group 2 and the intermediate re-entrant rooted fold R4 and so connected with the root of the primary system that allows angular variation to take place :

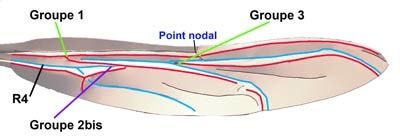A80

Note that the exiting group 2

 - Contains the widest orientation folds

- Has a particularly noticeable top because of

- Its accentuated relief Is relatively independent of the rest of the axial systems :

A41a

C.  Parts of the leading edge

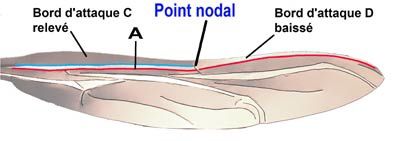A70b

The first exiting fold, A, is divided into two parts by the nodal point N. In the part nearest the thorax this fold starts as a re-entrant fold, extending from the wing root to the nodal point. This fold contravenes the folded surface geometrical theory i.e at the nodal point there should be a concentration of unusual forces, those produced by the transverse vein that forms the nodal point. This vein is not part of the fold structure system. It seems to be there for some other function.

Observation 1

The parts of the leading edge C and D are opposed. Their junction at the nodal point produces a twist between the two surfaces somewhat like the shape of a modern propeller, that is, the part nearest the thorax which has least angular mobility has a leading edge that is more efficient than the outer part of the wing. This description would apply to the majority of winged insects.

D. The posterior parts of the wing

 General profile of the wing :

 Sections (indicated in blue on A95) show that the profile of the wing levels out from the leading edge to the rear. Whereas the leading part is strongly folded, assuring the rigidity of the wingspan, folds on the rear surfaces have distinctly lower angles, conferring a degree of flexibility.

A95

A96

Closer study of the lower part of the wing (A96) reveals two surfaces, Pl1 and Pl2 which appear to have some mobility.

Pl1 behaves as a border surface capable of angular movement, considering the curve of the fold that puts a limit on the amount of travel

Pl2 Here there is a specific fold pA that breaks the structural fold pB  and seems to initiate a possible fracture. The dashes indicate a possible flexure of surface Pl2 resulting from various existing folds. Surface Pl2 thus appears to have some angular movement.

Considering the re-entrant folds concerned, it is worth noting that angular movement of the two surfaces is preferentially oriented towards the upper one.

Another possibility is the following :

If the structural folds of group 3 are relaxed, the discontinuous fold pB  (A96a) might be accentuated thus reducing the amount of travel of surface pl2

A96a

At present whether the dragonfly does utilise this rather subtle geometrical mechanism is unknown.

See section G movement of the wing in flight for a tentative description of the kinetics.

A further consideration :

A97

There is another structural weakness that runs through the node of the wing and continues through the re-entrant fold of group 3. The group 3 fold is indicated  (purple cross).

The possibility of major flexure of the wing is clear and is always upwards.

E. Angular freedom of movement :

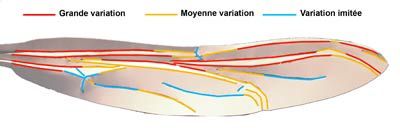A98

The overall geometrical composition of the wing is inhomogeneous. Certain folds, shown in red, may undergo maximum angular variation, approaching zero, particularly close to the wing root. Others, shown in blue, depend on the ability of the surrounding surfaces to curve, or impose strong geometrical nonlinearities on neighbouring folds.

A topology of flexibility of folding is clearly seen to develop. The forward part of the wing is freer, although blocked partially by the nodal point (shown in blue) The posterior part has weaker angular freedom of movement.

In a general way the rooted veins are seen broadly to control this gradation of freedom of movement.

F. How the folds are formed

 Here we set out several questions about the formation of folds to biologists.

 We have already posed as a principle of plication the question of spacing of the rooted wings capable of causing angular variation in the whole structure.

But for the folds of group 3, for example, this principle appears to encounter a certain limit to its continuity, given that several folds are not rooted and only slightly influenced by the angular variations  of other groups.

Hence another way of forming or varying the folds has to be envisaged, starting with the functioning of the veins themselves.

Question 1 : Is the angular configuration of the folds of the vein system rigid, semi-rigid, or loose?

Question 2 : According to existing studies that I have found, the nerve system is formed from a tube which is filled with haemolymphatic liquid at the point of emergence and whose pressure forms the completed structure of the wing.

Is the haemolymphic pressure constant after emergence?

Is the tube forming the vein structure made of an expandable or contractible material capable of varying the angle of the folds?

overpressure - underpressure

A100  A101

Biosimulation condidered

Biosimulation, of which one says little, if with enthusiasm, is used ostensibly secretly in industry. I rather think it is still regarded as shameful, or childish. Technology has produced a dogmatic mind-set still quite difficult to counter these days. However, Leonardo de Vinci long ago practised biosimulation when inspired by a bird’s wing to design the first aircraft. Galileo comprehended the movement of the earth by observing the satellites of Jupiter! Biosimulation not only concerns nature but also stimulates much research in biology, botany, geology etc. Furthermore, biosimulation has brought into being a biotechnology that is concerned with every sort of form, whether natural or artificial, inventing things itself and greatly stimulating research in biology. It is a new field of imagination dating back several years. The most innovative structures are founded on the principles of origami, a “minor art” from the East.

This “biotechnology stance” helps us go extend our hypotheses, starting with our observations on the dragonfly wing, towards technical inventions that may be rediscovered in the animal world itself.

With a vein system formed by two parallel tubes, one on the outside of the fold and the other on the inside :

variations in pressure between the two tubes would allow precise control of the angular variation of the fold :

differential adjustment -   

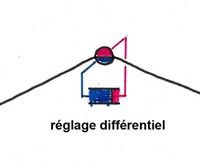A102    A103

Here we cannot help mentioning the phenomenon of plants with retractile leaves, and think of a similar mechanism of haemolymphatic liquid pressure variation in insects.

G. Movement of the wing in flight

The configuration of the wing roots, as we have seen, is distinctive. In detail the embedding of the wing roots seems to be more complex.

It is a matter of seeing how this set of four wing roots is set in motion by the beating of the wing, and what are the consequences of angular variation of the folds.

The wing rests on a pivot about which it lifts up and down depending on the force exerted by the levator or depressor muscles situated in one place or another on the pivot.

Reference: Dijkstra, K-D.B. Guide to the dragonflies of France and Europe. Ed. Guides du Naturaliste. (Illustrations by R. Lewington).

- It is known that the dragonfly has a set of muscles comprising:

- A wing levator muscle

- A large anterior wing depressor muscle for serving rapid flight

- A large posterior wing depressor muscle for hovering

- Two depressor muscles working together for normal flight

- 4 small supplementary muscles in a group to generate variable twisting of the wings for sudden movements, vertical lift etc.

A biosimulation study that I have in mind to write up shows dragonfly flight in slow motion. The movement of the dragonfly wing is different from that of other winged insects. The latter show a complex figure-of-eight torsional movement, whereas dragonfly wings beat only in a vertical plane, with alternation of the anterior and posterior wings.

The resulting dynamic shows as a rising vortex that keeps the dragonfly in the air. I cannot say more at present as I am awaiting comment from other researchers but I can at least say that the wing folds are not inconsequential to this aerodynamic system of propulsion.

H. Iridescence and angular variations

Recently the research worker Ekaterina Shevstova, collegues from the University of Lund in Sweden and biologists from the University of Pennsylvania (Science and Life No. 1123, April 2011), have discovered that the wings of flying insects have iridescent surfaces, visible when seen against a dark background. It is known that the colour of a ray entering and leaving surface micro-pits varies according to the change in the angle of incidence. It is therefore quite possible to imagine that the varying angles of the sections produced by the folds of the dragonfly wing might produce distinct patterns. If in addition these angles are variable on can imagine that the dragonflies might “read” the condition of the individual displayed.